Home  ›  what is the ratio of mean velocity to maximum velocity?

what is the ratio of mean velocity to maximum velocity?

Written By Saturday, April 9, 2022 Add Comment Edit
next up previous
Next: Effusion Up: Applications of Statistical Thermodynamics Previous: Specific Heats of Solids

Maxwell Velocity Distribution

Consider a molecule of mass 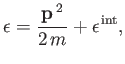$ m$ in a gas that is sufficiently dilute for the intermolecular forces to exist negligible (i.e., an platonic gas). The energy of the molecule is written
$\displaystyle \epsilon = \frac{{\bf p}^{ 2}}{2 m} + \epsilon^{ \rm int},$ (seven.202)

where $ \bf p$ is its momentum vector, and $ \epsilon^{ \rm int}$ is its internal (i.due east., non-translational) free energy. The latter energy is due to molecular rotation, vibration, et cetera. Translational degrees of freedom can exist treated classically to an fantabulous approximation, whereas internal degrees of freedom usually require a quantum-mechanical approach. Classically, the probability of finding the molecule in a given internal state with a position vector in the range $ \bf r$ to $ {\bf r} + d{\bf r}$ , and a momentum vector in the range $ \bf p$ to $ {\bf p} + d{\bf p}$ , is proportional to the number of cells (of ``volume'' $ h_0$ ) contained in the respective region of phase-infinite, weighted past the Boltzmann gene. In fact, because classical phase-space is divided upwards into uniform cells, the number of cells is simply proportional to the ``volume'' of the region under consideration. This ``volume'' is written $ d^{ 3}{\bf r} d^{ 3}{\bf p}$ . Thus, the probability of finding the molecule in a given internal state $ s$ is
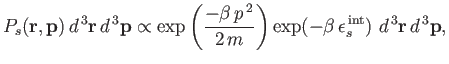$\displaystyle P_s({\bf r}, {\bf p}) d^{ 3}{\bf r} d^{ 3}{\bf p} \propto \e... ...\right) \exp(-\beta \epsilon^{ \rm int}_s) d^{ 3}{\bf r} d^{ 3}{\bf p},$ (7.203)

where $ P_s$ is a probability density defined in the usual manner. The probability $ P({\bf r}, {\bf p}) d^{ 3}{\bf r} d^{ 3}{\bf p}$ of finding the molecule in whatsoever internal state with position and momentum vectors in the specified range is obtained past summing the previous expression over all possible internal states. The sum over $ \exp(-\beta \epsilon^{ \rm int}_s)$ just contributes a constant of proportionality (because the internal states do not depend on $ {\bf r}$ or $ {\bf p}$ ), so
$\displaystyle P({\bf r}, {\bf p}) d^{ 3}{\bf r} d^{ 3}{\bf p} \propto \exp\left(-\frac{\beta p^{ 2}}{2 m}\right) d^{ 3}{\bf r} d^{ 3}{\bf p}.$ (seven.204)

Of course, we tin can multiply this probability by the total number of molecules, $ N$ , in order to obtain the mean number of molecules with position and momentum vectors in the specified range.

Suppose that we at present wish to determine $ f({\bf r}, {\bf v}) d^{ 3}{\bf r} d^{ 3}{\bf v}$ : that is, the mean number of molecules with positions between $ {\bf r}$ and $ {\bf r} + d{\bf r}$ , and velocities in the range $ {\bf v}$ and $ {\bf v}+d{\bf v}$ . Considering $ {\bf v} = {\bf p}/m$ , it is easily seen that

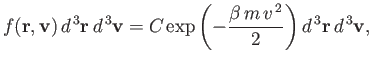$\displaystyle f({\bf r}, {\bf v}) d^{ 3}{\bf r} d^{ 3}{\bf v} = C \exp\left(-\frac{\beta m v^{ 2}}{2}\right) d^{ 3}{\bf r} d^{ 3}{\bf v},$ (7.205)

where $ C$ is a abiding of proportionality. This constant can be determined by the condition
$\displaystyle \int_{({\bf r})} \int_{({\bf v})} f({\bf r}, {\bf v}) d^{ 3}{\bf r} d^{ 3}{\bf v} = N.$ (7.206)

In other give-and-take, the sum over molecules with all possible positions and velocities gives the full number of molecules, $ N$ . The integral over the molecular position coordinates just gives the volume, $ V$ , of the gas, because the Boltzmann factor is independent of position. The integration over the velocity coordinates can exist reduced to the product of iii identical integrals (one for $ v_x$ , one for $ v_y$ , and ane for $ v_z$ ), so nosotros accept
$\displaystyle C V \left[\int_{-\infty}^{\infty} \exp\left(-\frac{\beta m v_z^{ 2}}{2}\right) dv_z\right]^{ 3} = N.$ (7.207)

Now,
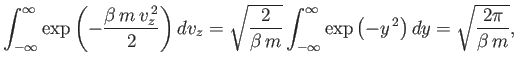$\displaystyle \int_{-\infty}^{\infty} \exp\left(-\frac{\beta m v_z^{ 2}}{2}... ...{-\infty}^{\infty} \exp\left(-y^{ 2}\right)dy = \sqrt{\frac{2\pi}{\beta m}},$ (vii.208)

and so $ C =(N/V) (\beta m / 2\pi)^{3/2}$ . (See Exercise two.) Thus, the properly normalized distribution function for molecular velocities is written
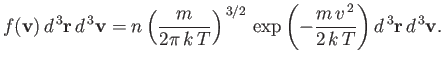$\displaystyle f({\bf v}) d^{ 3}{\bf r} d^{ 3}{\bf v} = n \left(\frac{m}{2\... ..., \exp\left(-\frac{m v^{ 2}}{ 2 k T}\right)d^{ 3}{\bf r} d^{ 3}{\bf v}.$ (7.209)

Here, $ n=N/V$ is the number density of the molecules. Nosotros have omitted the variable $ {\bf r}$ in the argument of $ f$ , because $ f$ clearly does non depend on position. In other words, the distribution of molecular velocities is uniform in space. This is hardly surprising, because there is nothing to distinguish i region of space from some other in our calculation. The previous distribution is chosen the Maxwell velocity distribution, because it was discovered by James Clark Maxwell in the middle of the nineteenth century. The average number of molecules per unit book with velocities in the range $ {\bf v}$ to $ {\bf v}+d{\bf v}$ is apparently $ f({\bf v}) d^{ 3}{\bf v}$ .

Let united states consider the distribution of a given component of velocity: the $ z$ -component (say). Suppose that $ g(v_z) dv_z$ is the average number of molecules per unit volume with the $ z$ -component of velocity in the range $ v_z$ to $ v_z+dv_z$ , irrespective of the values of their other velocity components. It is fairly obvious that this distribution is obtained from the Maxwell distribution by summing (integrating actually) over all possible values of $ v_x$ and $ v_y$ , with $ v_z$ in the specified range. Thus,

$\displaystyle g(v_z) dv_z = \int_{(v_x)} \int_{(v_y)} f({\bf v}) d^{ 3}{\bf v}.$ (vii.210)

This gives
or
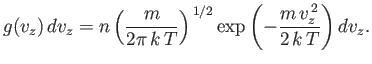$\displaystyle g(v_z) dv_z = n \left(\frac{m}{2\pi k T} \right)^{ 1/2} \exp\left(-\frac{m v_z^{ 2}}{2 k T}\right) dv_z.$ (vii.212)

Of course, this expression is properly normalized, so that
$\displaystyle \int_{-\infty}^{\infty} g(v_z) dv_z = n.$ (7.213)

Information technology is clear that each component (because there is nothing special about the $ z$ -component) of the velocity is distributed with a Gaussian probability distribution (see Department ii.9), centered on a mean value

$\displaystyle \overline{v_z} = 0,$ (7.214)

with variance
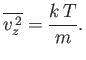$\displaystyle \overline{v_z^{ 2}} = \frac{k T}{m}.$ (7.215)

Equation (7.214) implies that each molecule is just as likely to exist moving in the plus $ z$ -direction as in the minus $ z$ -direction. Equation (7.215) can be rearranged to give
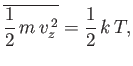$\displaystyle \overline{\frac{1}{2} m v_z^{ 2}} = \frac{1}{2} k T,$ (7.216)

in accordance with the equipartition theorem.

Note that Equation (7.209) can be rewritten

$\displaystyle \frac{ f({\bf v}) d^{ 3}{\bf v}}{n} =\left[\frac{g(v_x) dv_x... ...\right] \left[\frac{g(v_y) dv_y}{n}\right]\left[\frac{g(v_z) dv_z}{n}\right],$ (7.217)

where $ g(v_x)$ and $ g(v_y)$ are defined in an analogous way to $ g(v_z)$ . Thus, the probability that the velocity lies in the range $ {\bf v}$ to $ {\bf v}+d{\bf v}$ is simply equal to the product of the probabilities that the velocity components lie in their respective ranges. In other words, the individual velocity components act like statistically-contained variables.

Suppose that we now wish to summate $ F(v) dv$ : that is, the boilerplate number of molecules per unit volume with a speed $ v=\vert{\bf v}\vert$ in the range $ v$ to $ v+dv$ . It is obvious that nosotros can obtain this quantity by summing over all molecules with speeds in this range, irrespective of the direction of their velocities. Thus,

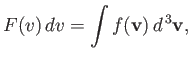$\displaystyle F(v) dv = \int f({\bf v}) d^{ 3}{\bf v},$ (7.218)

where the integral extends over all velocities satisfying
$\displaystyle v < \vert{\bf v}\vert < v + dv.$ (seven.219)

This inequality is satisfied by a spherical shell of radius $ v$ and thickness $ dv$ in velocity infinite. Because $ f({\bf v})$ merely depends on $ \vert v\vert$ , and so $ f({\bf v})\equiv f(v)$ , the previous integral is merely $ f(v)$ multiplied by the volume of the spherical shell in velocity space. So,
$\displaystyle F(v) dv = f(v) 4\pi v^{ 2} dv,$ (seven.220)

which gives
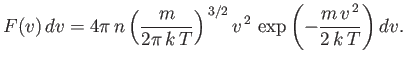$\displaystyle F(v) dv = 4\pi n\left(\frac{m}{2\pi k T}\right)^{ 3/2} v^{ 2} \exp\left(-\frac{m v^{ 2}}{2 k T}\right)dv.$ (7.221)

This is the famous Maxwell distribution of molecular speeds. Of course, it is properly normalized, so that
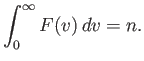$\displaystyle \int_0^\infty F(v) dv = n.$ (7.222)

Notation that the Maxwell distribution exhibits a maximum at some non-aught value of $ v$ . The reason for this is quite simple. Every bit $ v$ increases, the Boltzmann factor decreases, just the volume of phase-space available to the molecule (which is proportional to $ v^{ 2}$ ) increases: the internet outcome is a distribution with a non-zero maximum.
Figure: The Maxwell velocity distribution as a office of molecular speed, in units of the most probable speed ( $ \tilde{v}$ ). The dashed, dash-dotted, and dotted lines indicates the almost probable speed, the mean speed, and the root-mean-square speed, respectively.
\begin{figure} \epsfysize =3.5in \centerline{\epsffile{Chapter07/max.eps}} \end{figure}

The mean molecular speed is given by

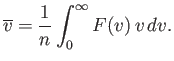$\displaystyle \overline{v} = \frac{1}{n} \int_0^\infty F(v) v dv.$ (vii.223)

Thus, we obtain
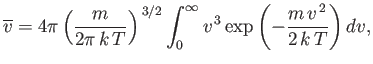$\displaystyle \overline{v} = 4\pi \left(\frac{m}{2\pi k T}\right)^{ 3/2} \int_0^\infty v^{ 3} \exp \left(-\frac{m v^{ 2}}{2 k T}\right)dv,$ (7.224)

or
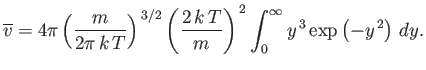$\displaystyle \overline{v} = 4\pi \left(\frac{m}{2\pi k T}\right)^{ 3/2} \l... ...c{2 k T}{m}\right)^{ 2} \int_0^\infty y^{ 3} \exp\left(-y^{ 2}\right) dy.$ (seven.225)

Now
$\displaystyle \int_0^\infty y^{ 3} \exp\left(-y^{ 2}\right)dy = \frac{1}{2}$ (7.226)

(see Do ii), so
$\displaystyle \overline{v} = \sqrt{\frac{8}{\pi} \frac{k T}{m}}.$ (vii.227)

A similar calculation gives
$\displaystyle v_{\rm rms} = \left[\overline{v^{ 2}}\right]^{ 1/2} = \sqrt{\frac{3 k T}{m}}.$ (7.228)

(See Exercise xiv.) All the same, this event tin also be obtained from the equipartition theorem. Because
$\displaystyle \overline{\frac{1}{2} m v^{ 2}} = \overline{\frac{1}{2} m (v_x^{ 2}+v_y^{ 2}+v_z^{ 2})} = 3 \left(\frac{1}{2} k T\right),$ (7.229)

then Equation (7.228) follows immediately. It is easily demonstrated that the most likely molecular speed (i.e., the maximum of the Maxwell distribution office) is
$\displaystyle \tilde{v} = \sqrt{\frac{2 k T}{m}}.$ (7.230)

The speed of sound in an ideal gas is given by
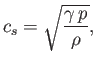$\displaystyle c_s = \sqrt{\frac{\gamma p}{\rho}},$ (7.231)

where $ \gamma$ is the ratio of specific heats. This can as well be written
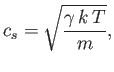$\displaystyle c_s=\sqrt{\frac{\gamma k T}{m}},$ (7.232)

considering $ p = n k T$ and $ \rho = n m$ . It is clear that the various average speeds that nosotros accept just calculated are all of order the sound speed (i.e., a few hundred meters per second at room temperature). In ordinary air ( $ \gamma=1.4$ ) the audio speed is about 84% of the most probable molecular speed, and about 74% of the mean molecular speed. Because sound waves ultimately propagate via molecular motion, information technology makes sense that they travel at slightly less than the most probable and hateful molecular speeds.

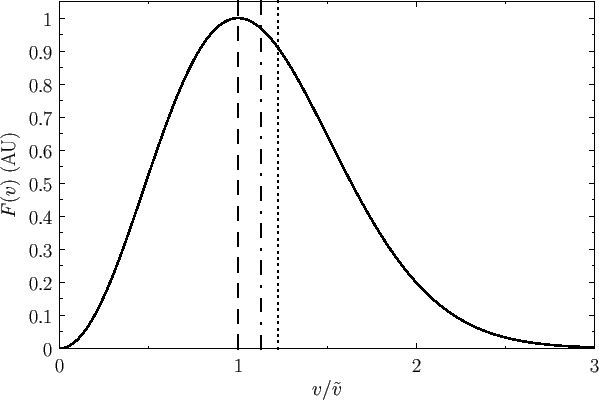
Figure 7.7 shows the Maxwell velocity distribution every bit a function of molecular speed in units of the most likely speed. Also shown are the mean speed and the root-mean-square speed.

next up previous
Next: Effusion Upwards: Applications of Statistical Thermodynamics Previous: Specific Heats of Solids
Richard Fitzpatrick 2016-01-25

johnsonlienshe.blogspot.com

Source: https://farside.ph.utexas.edu/teaching/sm1/Thermalhtml/node87.html

0 Response to "what is the ratio of mean velocity to maximum velocity?"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel